Semifinat kompetisi matematika nalaria realistik (KMNR 15) 2020 di Hartono Mall Solo Baru.
Segenap tenaga pengajar berfoto setelah selesai visitasi Akreditasi SMP Insan Cendekia Sukoharjo pada Agustus 2020.
Kunjungan Guru Matematika kabupaten Sukoharjo ke kantor PPPPTK Matematika Yogyakarta.
SMP Insan Cendekia menerima pendaftaran murid baru 2020/2021.
A. Syarat Pendaftaran
Syarat pendaftaran adalah sebagai berikut:
B. Waktu & Mekanisme Pendaftaran
Waktu Pendaftaran dimulai Bulan November 2019 sampai Kuota Telah terpenuhi
(per Februari 2020 Kuota masih tersedia)
Pendaftaran bisa dilakukan melalui:
Pendaftaran secara langsung
Pendaftaran Online:
SMP: DFT(Spasi)SMP(spasi)NAMA(spasi)Nominal(spasi)Tanggal Transfer(spasi)Waktu
kirim ke (087736037447).
C. Tempat
Pendaftaran secara langsung bisa dilayani di sekretariat Panitia Penerimaan Murid Baru (PMB), kampus SMP Insan Cendekia Boarding School Sukoharjo, Jl. Ovensari, Kadilangu, Baki, Sukoharjo, Jawa Tengah 57556. Telp (0271) 6727303
Peta Lokasi Klik di SINI.
D. Waktu dan Pelaksanaan Test
Pelaksaan Tes : One Day Service
Waktu tes : 3 Jam
Pendaftaran sewaktu-waktu bisa ditutup apabila kuota sudah terpenuhi.
E. DAFTAR ULANG
Peserta TSM yang dinyatakan lolos wajib melaksanakan proses Daftar Ulang (DU). Daftar ulang bisa dilakukan di sekretariat Panitia PMB, kampus SMA Insan Cendekia Boarding School Sukoharjo, Jl. Ovensari, Kadilangu, Baki, Sukoharjo, Jawa Tengah 57556. Dilayani pada setiap jam kerja, Senin-Jumat pukul 08.00-14.30 WIB dan hari Sabtu pukul 08.00-12.30 WIB.
F. BIAYA
Untuk biaya selengkapnya silahkan lihat di brosur pendaftaran
Sumber : http://smp.insancendekiaska.org/informasi-pendaftaran/
Matematika selama ini diajarkan dengan cara memberikan atau mentransformasikan langsung pengetahuan matematika kepada siswa, tanpa member kesempatan siswa untuk berpikir atau menelaah dari mana konsep atau rumus itu diperoleh. Hal tersebut membuat siswa kurang terasah penalarannya dan membuat siswa semakin sulit untuk memahami matematika di tingkat lanjut karena semakin tinggi tingkatan kelas, maka semakin butuh penalaran yang baik untuk memahami konsep matematika. Akibatnya, siswa yang tidak menguasai suatu konsep matematika akan semakin frustasi ketika harus mempelajari materi matematika berikutnya. Selain itu, penalara sangat penting bagi kehidupan karena penalaran yang baik dapat membantu untuk menganalisis masalah dalam kehidupan dengan lebih baik.
Matematika Nalaria Realistik (MNR) merupakan suatu terobosan baru dalam pembelajaran matematika. MNR lebih menekankan penggunaan nalar dalam memahami matematika, sehingga pembelajaran ini berbeda dengan pembelajaran matematika di sekolah. Dengan MNR, siswa diajarkan untuk menganalisis masalah, menarik kesimpulan dan menyelesaikan masalah dengan berbagai metode pemecahan masalah yang berlogika.
Ciri khas Matematika Nalaria Realistik:
v Menekankan penggunaan penalaran dalam memahami matematika
v Meningkatkan daya nalar dan keterampilan memecahkan masalah, khususnya dalam kehidupan sehari-hari.
Manfaat belajar Matematika Nalaria Realistik:
v Siswa akan lebih mudah memahami matematika
v Siswa akan terlatih penalarannya ketika belajar matematika
v Siswa akan lebih mudah memahami pelajaran lain karena nalarnya terasah.
v Siswa siap menghadapi berbagai kompetisi matematika
Langkah-langkah pengajaran Matematika Nalaria Realistik:
1. Pemberian masalah nyata
Dalam MNR siswa diberikan masalah nyata terlebih dahulu pada saat memulai pelajaran agar siswa tertarik untuk mengikuti materi tersebut karena terlibat dan merasa berkepentingan untuk mempelajarinya. Masalah nyata sebaiknya sesuai dengan pengetahuan yang dimiliki dan cara berpikir anak.
2. Pemahaman konsep
v Konsep matematika diberikan dengan melibatkan otak kiri dan kanan.
v Konsep matematika diajarkan tidak hanya menggunakan simbol-simbol matematika tetapi juga menggunakan gambar atau peraga matematika atau benda-benda yang ada di sekitar kita
v Setiap pokok bahasan mempunyai teknik pengajaran yang berbeda, oleh karena itu faktor guru menjadi sangat penting dalam penyampaian konsep-konsep matematika tersebut.
3. Penalaran dan komunikasi
v Melatih penalaran siswa dan melatih kemampuan siswa dalam mengkomunikasikan ide dan gagasannya
v Soal yang disajikan masih dalam lingkup materi yang sedang diajarkan
v Membiasakan siswa untuk berpikir sistematis dan mudah dipahami.
4. Pemecahan masalah
v Menyajikan soal yang merupakan gabungan berbagai konsep matematika yang sebelumnya sudah dipelajari
v Melatih keterampilan dalam memecahkan masalah dengan merekonstruksi materi yang sudah dipelajati sebelumnya
v Meningkatkan daya nalar siswa
v Meningkatkan kemampuan untuk menerima pengetahuan baru.
5. Aplikasi dalam kehidupan
v Menerapkan konsep matematika dalam kehidupan sehari-hari
v Siswa dapat mengetahui tujuan mempelajari suatu konsep matematika
v Memancing ketertarikan siswa untuk mempelajari materi berikutnya.
6. Eksplorasi matematika
v Melatih keterampilan psikomotorik
v Melatih mental siswa untuk berpikir kreatif dan patang menyerah
7. Permainan matematika
v Membuat siswa senang belajar matematika
v Mempermahir pemahaman konsep yang sudah dipahami.
Sumber : www.kpmseikhlasnya.com
Fibonacci adalah suatu barisan bilangan yang merupakan hasil penjumlahan dua bilangan sebelumnya.
Bilangan Fibonacci diperkenalkan pertama kali oleh Leonardo da Pisa atau yang lebih dikenal dengan Fibonacci pada abad ke 13.
Berikut akan dijelaskan mengenai contoh penerapan Fibonacci.
Fibonacci cukup banyak diterapkan dalam berbagai bidang. Dalam bidang ekonomi misalnya terdapat Teknik menentukan dan memprediksi pergerakan harga suatu produk dengan menggunakan Fibonacci.
Pada bagian sebelumnya telah dikemukakan bahwa bilangan Fibonacci merupakan penjumlahan dua bilangan sebelumnya.
Dua bilangan Fibonacci pertama yaitu bilangan 0 dan 1. Sehingga suku-suku berikutnya dari barisan bilangan Fibonacci yaitu sebagai berikut.
Bilangan pertama: 0
Bilangan kedua: 1
Bilangan ketiga: 0 + 1 = 1
Bilangan keempat: 1 + 1 = 2
Bilangan kelima: 1 + 2 = 3
Bilangan keenam: 2 + 3 = 5
Bilangan ketujuh: 3 + 5 = 8
Bilangan kedelapan: 5 + 8 = 13
dan seterusnya sehingga bilangan selanjutnya merupakan penjumlahan dari dua bilangan sebelumnya.
Selain itu, konsep Fibonacci juga digunakan digunakan untuk barisan bilangan yang lainnya. Perhatikan contoh di bawah ini.
4, 5, 9, 14, 23, . . .
Pada barisan di atas, suku pertama: 4 dan suku kedua: 5.
Suku ketiga: 4 + 5 = 9,
Suku keempat: 5 + 9 = 14,
Suku kelima: 9 + 14 = 23,
dan seterusnya.
Berikut akan dijelaskan mengenai deret Fibonacci.
Deret Fibonacci didefinisikan secara rekursif (berulang). Misalkan dalam beberapa pola barisan bilangan dengan dua suku pertama F1 = 0 dan F2 = 1.
Suku selanjutnya dirumuskan secara rekursif sebagai berikut.
Fn + 1 = Fn – 1 + Fn
Berikut ini akan dijelaskan mengenai rumus Fibonacci.
Untuk menentukan suku ke-n bilangan Fibonacci dapat dengan menggunakan rumus berikut ini.
fn = 1/√5 x ((1 + √5)/2)n – 1/√5 x ((1 – √5)/2)n
Membantu menjaga stamina tubuh
Komposisi :
Instan coffee powder, non dairy creamer, gingseng extract powder, cordyceps, purwaceng, red beet
Competitive edge :
 |
Kesebangunan dan kekongruenan merupakan bagian dari ilmu geometri. Materi yang akan disampaikan meliputi kesebangunan dan kekongruenan. Bangun datar yang akan dibahas meliputi segitiga dan trapesium. Materi mengenai kesebangunan dan kekongruenan sering muncul dalam kisi – kisi ujian nasional tingkat SMP/MTs/Sederajat. Materinya cukup mudah untuk dipelajari.
Materi kesebangunan memungkinkan seseorang menghitung lebar sungai tanpa mengukurnya. Selain itu juga dapat digunakan untuk menghitung tinggi gedung. Bagaimana bisa? Lihat contoh soal kesebangunan yang mengulas materi tersebut pada akhir bagian halaman ini. Sebelumnya, simak terlebih dahulu penjelasan kesebangunan dan kekongruenan pada masing – masing bahasan berikut. Apakah perbedaan kesebangunan dan kekongruenan? Cari lebih lanjut pada bahasan di bawah.
Kesebangunan disimbolkan dengan ‘ ~ ‘ yang bisa dibaca sebangun. Misalkan diberikan dua buah bangun datar segitiga ABC dan segitiga DEF. Maka jika terdapat tulisan ∆ABC ~ ∆ DEF dapat diartikan bahwa dua buah segitiga tersebut sebangun.
Dua buah bangun datar dikatakan sebangun jika memiliki besar sudut yang bersesuaian sama besar. Selain itu, perbandingan panjang sisi – sisi yang bersesuaian pada dua buah bangun datar tersebut juga sama.
Kesimpulannya, hubungan antara dua bangun datar dikatakan sebangun jika memenuhi syarat berikut.
Terdapat beberapa bentuk kesebangunan pada bidang datar, baik untuk bidang datar berbentuk segitiga atau bidang datar segi empat seperti pada trapesium. Berikut ini persamaan yang dihasilkan melalui kesebangunan pada kedua jenis bangun tersebut.
Kesebangunan pada Segitiga:
Bentuk 1: kesebangunan pada segitiga
![\[ \frac{AD}{AB} = \frac{AE}{AC} = \frac{DE}{BC} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-42354954c99c99281faafe9d3e526b4f_l3.png "Rendered by QuickLaTeX.com")
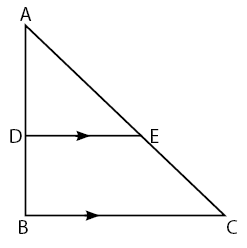
atau
![\[ \frac{AD}{DB} = \frac{AE}{EC} =\frac{DE}{BC - DE} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-b4c7e0b8403920e0f7a3da9fa42db32f_l3.png "Rendered by QuickLaTeX.com")
Bentuk 2: kesebangunan pada segitiga
![\[BC^{2} = CD \times CA \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-58817262a5786ddbd217c4a6bc793a54_l3.png "Rendered by QuickLaTeX.com")
![\[BA^{2} = AD \times AC \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-079e63212e2cc75d82dac83fffcbb322_l3.png "Rendered by QuickLaTeX.com")
![\[BD^{2} = DA \times DC \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-e0439b823acdb69bae866d43ce5c211f_l3.png "Rendered by QuickLaTeX.com")
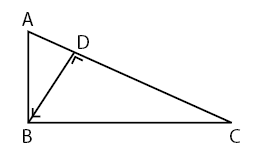
Berikutnya adalah kesebangunan pada bidang datar segi empat yaitu bangun datar berbentuk trapesium. Ada dua bentuk yang perlu sobat idschool ketahui.
Kesebangunan pada Trapesium
Bentuk 1: kesebangunan pada trapesium
![\[ EF = \frac{(DC \times AE) + (AB \times DE)}{AE + DE} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-32b2759696573c5a65bb1e77cb6fcd0a_l3.png "Rendered by QuickLaTeX.com")
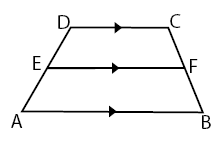
atau
![\[ EF = \frac{(DC \times BF)+ (AB \times CF)}{CF + BF} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-08b7d580902a5242362c7643966eb7d8_l3.png "Rendered by QuickLaTeX.com")
Bentuk 2: kesebangunan pada trapesium
![\[EF =\frac{1}{2} \left(AB - CD \right) \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-23da3403b032aafb5175dd6735636b11_l3.png "Rendered by QuickLaTeX.com")
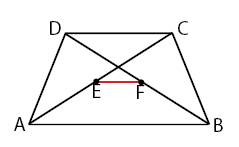
Keterangan: E dan F berturut-turut adalah titik tengah AC dan BD.
Kedua rumus kesebangunan pada trapesium di atas diperoleh melalui penyederhanaan persamaan. Lihat penurunan rumus kesebangunan trapesium halaman ini. Kedua rumus yang diperoleh tersebut melibatkan persamaan perbandingan sisi untuk dua bangun yang sebangun.
Itulah tadi ulasan materi kesebangunan dan kegunaannya untuk menghitung panjang sisi yang belum diketahui. Untuk lebih jelasnya, sobat idschool bisa melihat penggunaan rumus tersebut pada contoh soal kesebangunan yang akan diberikan pada akhir bahasan.
Namun sebelumnya, akan diulas materi kekongruenan terlebih dahulu. Apa itu kongruen? Apakah kongruen sama dengan sebangun? Simak ulasan kekongruenan berikut.
Dua benda atau lebih dikatakan kongruen jika memiliki bentuk dan
ukuran yang sama. Dua buah bangun yang kongruen dihubungkan melalui
simbol kongruen. Bagaimanakah simbol kongruen? Kekongruenan dilambangkan
dengan 
.
Misalkan diberikan dua buah bangun segitiga yaitu ∆ABC dan ∆DEF.
Kedua segitiga tersebut diketahui memiliki ukuran dan bentuk yang sama.
Sehingga dapat dikatakan bahwa ∆ABC dan ∆DEF adalah kongruen. Penulisan
yang menyatakan bahwa dua segitiga tersebut kongruen adalah ∆ABC ∆ DEF. Dibaca segitiga ABC kongruen dengan segitiga DEF.
Syarat Kekongruenan pada segitiga:
Pelajari kekongruenan melalui contoh sederhana berikut. Perhatikan gambar segitiga di bawah!
Pasangan segitiga yang kongruen pada di atas tersebut adalah
![\[ \Delta ABG \cong \Delta EDH \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-bec297d6428ca9214af379d97c55b5ea_l3.png "Rendered by QuickLaTeX.com")
![\[ \Delta BGC \cong \Delta DHC \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-10f2e825232ec89006e0f009a2183234_l3.png "Rendered by QuickLaTeX.com")
![\[ \Delta ABF \cong \Delta DFE \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-56521741d22e098da7bba183615b1dfa_l3.png "Rendered by QuickLaTeX.com")
![\[ \Delta ACD \cong \Delta ECB \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-0dceac0582231237ab66286057b7f364_l3.png "Rendered by QuickLaTeX.com")
![\[ \Delta ABC \cong \Delta EDC \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-b1fcc1fc6aae20a0b82dc3413f7628cc_l3.png "Rendered by QuickLaTeX.com")
![\[ \Delta ABD \cong \Delta EDB \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-22279a72960e99c023493e0aeeb3d104_l3.png "Rendered by QuickLaTeX.com")
![\[ \Delta AGF \cong \Delta EHF \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-49b309e7708f01b9337e8ee5e881e9a7_l3.png "Rendered by QuickLaTeX.com")
![\[ \Delta ACH \cong \Delta EGC \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-09ce67f18f076d828a130aad0aa0f0ae_l3.png "Rendered by QuickLaTeX.com")
Jadi, banyaknya segitiga yang kongruen ada 8 pasang.
Itulah tadi bahasan mengenai materi kesebangunan dan kekongruenan. Kesimpulan yang dapat diambil adalah, dua bangun datar yang sebangun belum tentu merupakan dua bangun datar yang saling kongruen. Namun, dua bangun datar yang kongruen pasti merupakan dua bangun datar yang sebangun.
Berikut ini penggunaan konsep kesebangunan untuk menyelesaikan berbagai permasalahan. Simak contoh soal kesebangunan dan pembahasan nya berikut.
Variasi soal pada kesebangunan dan kekongruenan sangat banyak. Berikut ini ada tiga tipe contoh soal yang keluar di Ujian Nasional beserta pembahasannya.
Pembahasan:
Perhatikan gambar berikut!
Perhatikan segitiga ABE dan segitiga ACD!
Berdasarkan prinsip kesebangunan dapat diperoleh
![\[ \frac{EB}{DC} = \frac{AB}{AC} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-3a0e89fa7fe70895c90e36cd6d8693af_l3.png "Rendered by QuickLaTeX.com")
Sehingga,
![\[\frac{1,5}{DC} = \frac{4}{14} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-d0daf92b4b360c8a272895b3aca305d9_l3.png "Rendered by QuickLaTeX.com")
![\[DC = \frac{1,5 \times 14}{4} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-329a986cf59cbc3866f415c18387785c_l3.png "Rendered by QuickLaTeX.com")
![\[DC = 5,25 \; m \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-8258a322e537dbf804eb69f9b1215cb7_l3.png "Rendered by QuickLaTeX.com")
Jawaban: A
Perhatikan gambar berikut!
Jika CF : FB = 2 : 3 dan CD = 12 cm, maka panjang EF adalah …. (SOAL UN MATEMATIKA SMP 2016)
A. 6 cm
B. 9 cm
C. 12 cm
D. 18 cm
Pembahasan:
Berdasarkan keterangan pada soal, kita dapat mengetahui ukuran masing-masing sisi, seperti terlihat pada gambar berikut.
Untuk menghitung EF, gunakan rumus di bawah.
![\[EF =\frac{CD \times FB + AB \times CF}{FB + CF} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-72073a0d1110ffaf09bf30388bb11456_l3.png "Rendered by QuickLaTeX.com")
Sehingga,
![\[EF =\frac{12 \times 3x + 27 \times 2x}{3x + 2x} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-508325d8a6c26026e4349f179a407397_l3.png "Rendered by QuickLaTeX.com")
![\[EF =\frac{36x + 54x}{5x} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-3ff11853f7f5f3db79c58247619fc16f_l3.png "Rendered by QuickLaTeX.com")
![\[EF =\frac{90x}{5x}\;=\;18\;cm \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-5f870806cc200cc03da10ee0ea46ae4e_l3.png "Rendered by QuickLaTeX.com")
Jawaban: D
Baca Juga: Skala, Jarak pada Peta, dan Jarak Sebenarnya
“Lebar Sungai”
Andi ingin mengetahui lebar sungai. Di seberang sungai terdapat sebuah pohon. Untuk itu dia menancapkan tongkat sehingga berada pada posisi A, B, C, dan D dengan ukuran seperti pada gambar.
Andi ingin mengukur lebar sungai dari tongkat D sampai pohon. Berapa lebar sungai tersebut? (SOAL UN MATEMATIKA SMP 2016)
A. 11 m
B. 12 m
C. 15 m
D. 16 m
Pembahasan:
Perhatikan sketsa berikut!
Baca Juga: Sistem Persamaan Linear Dua Variabel – SPLDV
Lebar sungai dapat dihitung dengan memanfaatkan kesebangunan segitiga.
Lebar sungai = DP
![\[ \frac{DP}{AP} = \frac{DC}{AB} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-19e94d7ae962ceb9ac7403795e2426c1_l3.png "Rendered by QuickLaTeX.com")
![\[ \frac{DP}{4 + DP} = \frac{6}{8} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-d3017360770749b323b0b9bdaac2f3c6_l3.png "Rendered by QuickLaTeX.com")
![\[ 8DP = 6 \times (4 + DP) \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-be7ab78fc559f7c822ed366e200e0998_l3.png "Rendered by QuickLaTeX.com")
![\[ 8DP = 24 + 6DP) \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-d0747c448043e0660833cead60fd0dd1_l3.png "Rendered by QuickLaTeX.com")
![\[ 8DP - 6DP = 24 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-7cc10d3205b9671119eab5e411218bfb_l3.png "Rendered by QuickLaTeX.com")
![\[ 2DP = 24 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-a1405b6a845451da884fc211a0076537_l3.png "Rendered by QuickLaTeX.com")
![\[ DP = \frac{24}{2} = 12 \; m \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-fb355efecdaa75c5cf809062ed5f0f3e_l3.png "Rendered by QuickLaTeX.com")
Jadi, lebar sungai = DP = 12 m.
Jawaban: B
Sekian ulasan materi mengenai kesebangunan dan kekongruenan. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
.png)
